Picard theorem
- For the theorem on existence and uniqueness of solutions of differential equations, see Picard's existence theorem.
In complex analysis, the term Picard theorem (named after Charles Émile Picard) refers to either of two distinct yet related theorems, both of which pertain to the range of an analytic function.
Contents |
Statement of the theorems
Little Picard
The first theorem, also referred to as "Little Picard", states that if a complex function f(z) is entire and non-constant, then the set of values that f(z) assumes is either the whole complex plane or the plane minus a single point.
This theorem was proved by Picard in 1879. It is a significant strengthening of Liouville's theorem which states that the image of an entire non-constant function must be unbounded.
Overview of the proof
We call X the Riemann surface consisting of a plane minus two points, and 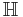 the upper half-space, on which the modular group
the upper half-space, on which the modular group 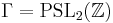 acts by Moebius transformations. From the theory of modular curves, the j-invariant is a holomorphic map from the upper half-space
acts by Moebius transformations. From the theory of modular curves, the j-invariant is a holomorphic map from the upper half-space 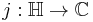 that is invariant under the action of
that is invariant under the action of 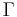 . Its derivative
. Its derivative 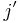 vanishes only on the orbit of i and
vanishes only on the orbit of i and 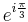 , so that its restriction to
, so that its restriction to 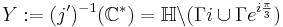 induces a covering map
induces a covering map 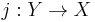 .
.
This covering space is isomorphic to an open set of the disc, as the half plane and the disc are conformally equivalent (see Moebius transformation#Subgroups of the Moebius group).
Suppose now that we have an entire function f which misses two points. This function can be thought of as a map 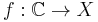 , and can therefore be factored by the cover j holomorphically to the disc. This gives a bounded map holomorphic map from the plane to itself, which, by Liouville theorem, is therefore constant hence the original function f must have been constant.
, and can therefore be factored by the cover j holomorphically to the disc. This gives a bounded map holomorphic map from the plane to itself, which, by Liouville theorem, is therefore constant hence the original function f must have been constant.
Big Picard
The second theorem, also called "Big Picard" or "Great Picard", states that if an analytic function f(z) has an essential singularity at a point w, then on any open set containing w, the function f(z) takes on all possible complex values, with at most a single exception, infinitely often.
This is a substantial strengthening of the Weierstrass–Casorati theorem, which only guarantees that the range of f is dense in the complex plane.
Notes
- The "single exception" is in fact needed in both theorems: ez is an entire non-constant function which is never 0, and e1/z has an essential singularity at 0, but still never attains 0 as a value.
- Big Picard is true in a slightly more general form that also applies to meromorphic functions: if M is a Riemann surface, w is a point on M, P1C = C∪{∞} denotes the Riemann sphere and f : M \ {w} → P1C is a holomorphic function with essential singularity at w, then on any open subset of M that contains w the function f attains all but at most two points of P1C infinitely often.
- As an example, the meromorphic function f(z) = 1/(1 − exp(1/z)) has an essential singularity at z = 0 and attains the value ∞ infinitely often in any neighborhood of 0; however it does not attain the values 0 or 1.
- With this generalization, Little Picard follows from Big Picard because an entire function is either a polynomial or it has an essential singularity at infinity.
- The following conjecture[1] is related to "Big Picard": Let D \ {0} be the punctured unit disk in the complex plane and let U1, U2, ..., Un be a finite cover of D \ {0} by open connected sets Uj. Suppose that on each Uj there is an injective holomorphic function fj, such that dfj = dfk on each intersection Uj ∩ Uk. Then the differentials glue together to a meromorphic 1-form on the unit disk
 . (It is clear that the differentials glue together to a holomorphic 1-form g dz on D \ {0} . In the special case where the residue of g at 0 is zero, then the conjecture follows from "Big Picard".)
. (It is clear that the differentials glue together to a holomorphic 1-form g dz on D \ {0} . In the special case where the residue of g at 0 is zero, then the conjecture follows from "Big Picard".)
Notes
- ^ Elsner, B. (1999). "Hyperelliptic action integral". Annales de l'institut Fourier 49 (1): 303–331. doi:10.5802/aif.1675. http://archive.numdam.org/ARCHIVE/AIF/AIF_1999__49_1/AIF_1999__49_1_303_0/AIF_1999__49_1_303_0.pdf.
References
- Conway, John B. (1978). Functions of One Complex Variable I (2nd ed.). Springer. ISBN 0-387-90328-3.
- Shurman, Jerry. "Sketch of Picard's Theorem". http://people.reed.edu/~jerry/311/picard.pdf. Retrieved 2010-05-18.